Don't Roll Your Own Crypto #1
28 Juli 2021 • ☕️☕️☕️ 13 min read
Available other languages: Bahasa Indonesia
Read in English • View all translated posts
Introduction
Ini adalah sebuah series dimana saya akan mencoba melakukan kriptanalisis terhadap skema kriptosistem yang diusulkan pada berbagai jurnal, paper, maupun artikel akademis dari beberapa Universitas di Indonesia.
Tulisan ini hanya berusaha menekankan pada kalimat “Don’t roll your own Crypto”, dimana lebih baik kita menggunakan algoritma kriptografi yang sudah distandarisasi dibandingkan merancang algoritma sendiri yang belum terbukti keamanannya.
Ini bukan berarti saya meng-encourage akademisi untuk tidak mengusulkan algoritma sendiri ya, tapi ini lebih ditargetkan kepada developer atau pelaksana dalam IT security untuk tidak sembarangan memilih atau merancang sebuah kriptosistem.
Selain itu, tulisan ini juga tidak ada niatan sama sekali untuk merendahkan penelitian-penelitian yang berkaitan. Bagaimanapun juga, memang seperti inilah proses pengusulan sebuah skema kriptosistem dilakukan, dimana ada satu pihak mengusulkan ide, pihak-pihak lainnya akan mencoba mencari kelemahan dari ide tersebut, hingga akhirnya dari kelemahan-kelemahan tersebut dapat dikembangkan menjadi skema yang lebih baik lagi dan begitu seterusnya.
Chaos-based Image Encryption
Skema kriptosistem yang akan dibahas di seri pertama kali ini adalah penelitian dari artikel yang berjudul “ANALISIS KEAMANAN ALGORITMA ENKRIPSI CITRA DIGITAL MENGGUNAKAN KOMBINASI DUA CHAOS MAP DAN PENERAPAN TEKNIK SELEKTIF” oleh Rinaldi Munir, yang dipublikasikan oleh Jurnal Ilmiah Teknologi Informasi (JUTI) pada tahun 2012 [1].
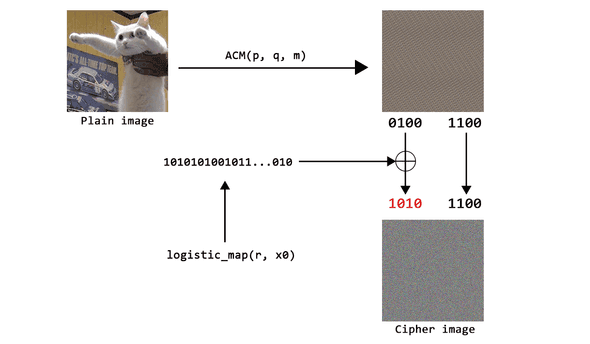
Artikel tersebut membahas mengenai algoritma enkripsi gambar dengan memanfaatkan dua fungsi Chaos, yaitu Arnold Cat Map sebagai fungsi permutasi dan Logistic Map sebagai pembangkit keystream.
Selain itu, dijelaskan juga penggunaan “enkripsi selektif” dimana enkripsi hanya dilakukan pada 4-bit awal (Most Significant Byte) saja, sedangkan 4-bit akhir (Least Significant Byte) pada gambar (setelah dipermutasi) tidak akan berubah.
Arnold’s Cat Map
Arnold’s Cat Map (ACM) adalah fungsi Chaos Map untuk mengacak posisi pixel-pixel (dalam koordinat x dan y) pada sebuah gambar.
Persamaan ACM yang dipakai dalam artikel tersebut adalah sebagai berikut.
Dimana (x,y) adalah posisi pixel awal dan (x',y') adalah posisi pixel setelah dipermutasi. Sementara itu, nilai N adalah ukuran panjang dari gambar. Fungsi ini akan dijalankan sebanyak m kali.
Jadi, secret variable yang ada pada fungsi ACM terdiri dari p, q, dan m.
Berikut adalah visualisasi gambar setelah dilakukan fungsi ACM beberapa kali, terlihat semakin tinggi nilai m, semakin terlihat acak hasil posisi pixel-nya.
Untuk membalik proses ACM, kita cukup mengkalikan (x',y') dengan invers matriks .
Logistic Map
Logistic Map adalah fungsi Chaos Map yang dihasilkan dari persamaan non-linear sederhana berikut.
Dimana didefinisikan r sebagai konstanta bilangan real dalam interval 0 hingga 4 dan x0 sebagai nilai awal acak dalam interval 0 hingga 1. Kedua variabel ini dirahasiakan nilainya.
Untuk membangkitkan keystream menggunakan Logistic Map, cukup kalkulasikan persamaan diatas yang menghasilkan x1, x2, x3, ... hingga panjang keystream yang dibutuhkan terpenuhi. Nilai pada x1, x2, x3, ... masing-masing merepresentasikan 4-bit kunci yang diambil dari nilai dibelakang koma.
Misalnya dihasilkan deretan dari Logistic Map yaitu 0.5, 0.875, 0.3828125, 0.8269348, ..., maka diambil beberapa angka dibelakang koma menjadi 5, 875, 3828, 8269, ..., ubah masing-masing ke binary dan ambil 4-bit terakhir (LSB) menghasilkan keystream 0101, 1011, 0100, 1101, ....
Encryption
Tahapan enkripsinya secara singkat adalah sebagai berikut.
- Inisialisasi Plain image
P, variabelp,q,m,r, danx0sebagai kunci rahasia. - Permutasi gambar
Pdengan fungsi Arnold Cat Map bersama parameterp,q, danm, menghasilkan gambarPx. - Gunakan Logistic Map untuk membangkitkan keystream
Kmenggunakan konstantardan nilai awalx0. - Enkripsi 4-bit MSB tiap pixel pada
Pxdengan keystreamKmenggunakan operasi XOR, menghasilkan 4-bitCxsetiap pixelnya. - Cipher image
Cyang didapatkan adalah gabungan hasil enkripsi 4-bitCxdengan 4-bit LSB pada gambarPx.
Implementasi enkripsi ini menggunakan Python dapat dilihat pada source disini
Cryptanalysis
Langsung saja kita coba lakukan kriptanalisis pada skema enkripsi gambar ini :D.
Dalam melakukan kriptanalisis, akan diasumsikan beberapa skenario implementasi dikarenakan dalam artikel tersebut tidak didefinisikan spesifikasi bagaimana implementasi seharusnya dilakukan.
Model kriptanalisis yang akan kita gunakan adalah Chosen-Plain image Attack, dimana kita dapat mengenkripsi gambar apapun yang kita mau sebanyak-banyaknya dan mendapatkan hasil Cipher image dari gambar tersebut.
Static Secret Key
Diasumsikan skenario implementasi dimana secret key yang terdiri variabel p, q, m, r, dan x0 bersifat statis dimana nilainya tidak berubah dalam eksekusi enkripsi yang berbeda.
Recovery of Keystream
Dikarenakan nilai r dan x0 selalu sama, hasil dari Logistic Map juga akan menghasilkan keystream yang sama juga.
Seperti pada stream cipher dimana keystream tidak boleh digunakan berulang kali, disini keystream (K) dapat di-extract dengan mudah selama kita mengetahui plain image yang telah dipermutasi dengan ACM (Px) dan cipher image-nya (C).
Namun disini kita tidak mengetahui nilai dari Px (hanya 4-bit LSB-nya saja yang diketahui) karena kita tidak diberikan parameter p, q, dan m pada ACM.
Well, karena ini adalah Chosen-Plain image Attack dan kita dapat mengenkripsi gambar apapun, kita tinggal gunakan Plain image yang mempunyai nilai sama disemua pixel-nya seperti gambar full hitam atau gambar full putih.
Karena semua nilai pixel pada gambar tersebut sama, maka permutasi ACM akan menghasilkan gambar yang sama juga, sehingga otomatis kita mengetahui nilai Px, lalu tinggal cari nilai keystream dengan operasi XOR ¯\_(ツ)_/¯
Setelah keystream didapatkan, mari kita cari nilai p, q, dan m.
Recovery of m
Perlu diketahui jika proses fungsi ACM sebenarnya cukup costly dalam sisi hardware, dimana dalam satu iterasi ACM saja (m=1) membutuhkan waktu yang tidak sebentar, sehingga perbedaan nilai m dengan m+1 cukup noticable.
Hal ini cukup berbahaya karena kita dapat mengetahui nilai m dari Timing Attack. Semakin tinggi nilai m yang digunakan, maka waktu yang dibutuhkan dalam operasi ACM akan memakan waktu lebih lama.
Terlebih, Timing Attack pada nilai m dapat dibuat sangat akurat dengan memakai ukuran gambar yang sangat besar, sehingga proses ACM pada satu iterasi m sangat besar.
Berikut adalah tabel hasil tes waktu yang dibutuhkan pada proses ACM menggunakan m = 1 hingga m = 5 pada gambar berukuran 1024x1024 menggunakan Laptop saya.
| m | Waktu (detik) |
|---|---|
| 1 | 7.1236 |
| 2 | 13.8878 |
| 3 | 21.7516 |
| 4 | 27.8001 |
| 5 | 35.2292 |
Dapat dilihat pada tabel tersebut bahwa waktu yang dibutuhkan relatif konsisten pada kelipatan 7 detik. Dari hal ini kita dapat menebak nilai m hanya dari waktu yang dibutuhkan dalam mengenkripsi gambar.
Sebenarnya dari awal, merahasiakan nilai m disini tidak relevan, karena bagaimanapun rentang nilai m tidak mungkin terlalu tinggi karena akan membawa performance issue pada enkripsinya jika terlalu tinggi. Jadi, kita pun dapat melakukan simple brute-force pada nilai m.
Recovery of p and q
Dengan didapatkannya nilai m, maka mencari p dan q cukup trivial.
Idenya adalah kita akan membuat sebuah Plain image yang semua pixelnya memiliki nilai warna hitam (0), kecuali pada satu koordinat saja memiliki warna putih (255) atau nilai selain 0.
Misalnya, kita tentukan pada koordinat (1, 0), maka Plain image yang berukuran 4x4 dapat direpresentasikan sebagai matrik berikut.
Masukkan plain image tersebut ke encryption oracle, didapatkan cipher image, dekripsi menggunakan keystream yang sudah kita dapatkan sebelumnya, sehingga kita memiliki plain-image yang telah dipermutasi.
Misalnya plain image yang dipermutasi tersebut adalah berikut.
Maka dapat kita simpulkan koordinat kita sebelumnya dari (1, 0) berpindah ke koordinat (2, 3).
Mari kita asumsikan nilai m = 3, maka persamaan ACM seperti yang dijelaskan sebelumnya menjadi berikut.
Kemudian dapat kita tuliskan menjadi:
Dimana nilai p dan q dapat dicari dengan menyelesaikan sistem persamaan linear dua variabel (dengan modulus N).
Akhirnya, dengan diketahui keystream K, nilai p, q, dan m pada ACM, kita dapat mendekripsi gambar apapun yang terenkripsi dibawah secret key ini :).
Proof of Concept
Mari kita buktikan dengan mengimplementasikannya kedalam Python.
Pertama, kita buat fungsi encryption_oracle() yang seolah-olah akan berperan sebagai “server” dimana kita dapat mengenkripsi gambar apapun ke “server” tersebut dan menerima cipher image-nya.
import random, os
import numpy as np
import encryption
from PIL import Image
from Crypto.Util.strxor import strxor
# Secret
p = random.randint(2,250)
q = random.randint(2,250)
m = 3
init = random.random()
r = 3 + random.random()
def encryption_oracle(plain_image):
return encryption.encrypt(plain_image, p, q, m, init, r)Lalu, buat fungsi recover_keystream untuk mendapatkan keystream dari chosen-plain image attack.
def recover_keystream(size):
# Generate full-black image
plain_image = Image.new("RGB", (size, size))
# Send image to encryption oracle
cipher_image = encryption_oracle(plain_image)
# Convert plain_image and cipher_image to bytes
plain_image_bytes = bytes(np.array(plain_image).flatten().tolist())
cipher_image_bytes = bytes(np.array(cipher_image).flatten().tolist())
# Recover 8-bit keystream
k = list(strxor(plain_image_bytes, cipher_image_bytes))
# Get 4-bit MSB keystream
keystream = []
for i in range(size**2):
bit_len = int(k[i]).bit_length()
if bit_len > 4:
msb = k[i] >> 4 & (2**(bit_len-4) - 1)
else:
msb = 0
keystream.append(msb)
return keystreamLalu, buat fungsi untuk mendapatkan m melalui Timing Attack.
def recover_m():
# avg. second of one encryption execution time (depends on the machine)
one_exec_time = 10
start_time = time.time()
payload = Image.new("RGB", (1024, 1024))
encryption_oracle(payload)
end_time = time.time()
elapsed_time = end_time - start_time
m = int(elapsed_time // one_exec_time)
# Result could be faster or slower
possible_m = [m, m-1, m+1]
return possible_mTerakhir, untuk mendapatkan nilai p dan q, kita akan menggunakan Sagemath dan menggunakan fungsi solve_mod() untuk menyelesaikan sistem persamaan yang dijelaskan sebelumnya.
#!/usr/bin/env sage
def recover_pq(m, x0, y0, x1, y1, N):
var('p,q')
xy = matrix(2,1,[x0,y0])
A = matrix([[1,p],[q, p*q + 1]])
pos_result = solve_mod([
(A^m * xy)[0][0] == x1,
(A^m * xy)[1][0] == y1
], N)
return pos_result
if __name__ == "__main__":
m = 7 # ACM iteration
x0 = 1
y0 = 0
x1 = 489 # x-coordinate after permutation
y2 = 396 # y-coordinate after permutation
N = 512 # image size
print("Possible p,q: ")
print(recover_pq(m, x0, y0, x1, y2, N))Implementasi lengkapnya dapat diakses di link ini.
Static Secret Key with Dynamic x0
Skenario implementasi berikutnya adalah jika diasumsikan variabel p,q,m,r bersifat statis namun variabel x0 dinamis, dimana nilai ini akan berubah-ubah dalam eksekusi enkripsi yang berbeda.
Skenario ini adalah skenario yang paling ideal yang dapat diimplementasikan pada skema kriptosistem ini, karena repeated keystream sudah tidak terjadi.
Namun, yang menjadi masalah adalah bagaimana nilai x0 ini dapat terbentuk dan terasosiasi disetiap gambar yang berbeda. Salah satu pendekatan yang mungkin dilakukan adalah dengan memperlakukan x0 ini seperti Initialization Vector (IV) seperti pada block cipher. Tapi, nilai ini harus tetap dienkripsi lagi dengan metode tertentu dan dicantumkan di setiap gambar yang telah terenkripsi menggunakan nilai tersebut.
Kita abaikan saja teknis bagaimana nilai x0 didistribusikan. Asumsi kita pada skenario ini adalah untuk setiap request ke encryption oracle, nilai x0 akan berubah-ubah dan bersifat acak.
Karena repeated keystream sudah tidak bisa dieksploitasi, maka akan sulit untuk kita mendapatkan keystream dari chosen-plain image attack, karena basically enkripsi ini menjadi One-Time Pad.
Recover ACM secret
Lalu bagaimana kita dapat mencari nilai p dan q tanpa mengetahui keystream yang digunakan?
Disinilah celah keamanan dari penggunaan ”enkripsi selektif” terjadi, dimana cipher image membocorkan informasi dari LSB plain image-nya.
Asumsikan kita menggunakan chosen-plain image yang direpresentasikan sebagai berikut.
Masukkan plain image tersebut ke encryption oracle. Kemudian, dimisalkan didapatkan cipher image sebagai berikut.
Kita ubah masing-masing pixel ke representasi binary dan boom!! LSB oracle goes brrrr!
Karena skema enkripsi selektif tersebut, kita masih mengetahui posisi koordinat pixel kita setelah dipermutasi karena 4-bit LSB dari plain image tidak pernah berubah (cukup perhatikan 4-bit LSB yang tidak bernilai 0000).
Tinggal lanjutkan menggunakan metode yang sama seperti skenario sebelumnya dengan menyelesaikan sistem persamaan dua variabel untuk mendapatkan nilai p dan q (nilai m masih bisa didapatkan melalui Timing Attack).
Selanjutnya, bagaimana kita dapat mencari nilai keystream yang dinamis? Sedangkan One-Time Pad merupakan unbreakable cipher.
Weak Logistic Map
Satu-satunya hal yang bisa kita coba eksploitasi adalah dari implementasi Logistic Map-nya.
Analisis mengenai bagaimana Logistic Map bekerja dijelaskan secara detail oleh blog dari geoffboeing.com [2]. Menariknya, ada beberapa hal yang dapat membuat hasil distribusi dari Logistic Map repititif dan periodik jika konstanta r dan nilai awal x0 tidak dipilih secara hati-hati.
Mari kita coba lakukan sedikit eksperimen menggunakan implementasi Logistic Map dari artikel ini dalam membangkitkan keystream.
import random
import encryption
for i in range(1000):
init = random.random()
r = random.randint(0,3) + random.random()
print('x0:', init)
print('r :', r)
print('keystream', encryption.logistic_map(init, r, 100, 10))
print()Jalankan script diatas dan kita coba ambil beberapa sampel hasil yang menarik.
x0: 0.7244972999777215
r : 2.2929146462509595
keystream: [7, 2, 15, 3, 5, 14, 0, 9, 1, 15, 7, 10, 0, 11, 10, 14, 6, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]
x0: 0.18893176526337663
r : 1.6653541535673568
keystream: [4, 9, 3, 1, 9, 7, 10, 8, 15, 15, 11, 7, 2, 15, 6, 12, 0, 8, 5, 15, 8, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12]
x0: 0.8927173285063715
r : 3.5157732279084075
keystream: [5, 13, 12, 12, 14, 5, 4, 0, 8, 0, 5, 8, 10, 0, 2, 11, 9, 0, 9, 7, 15, 2, 5, 14, 1, 2, 10, 15, 14, 11, 9, 15, 0, 9, 15, 7, 7, 13, 15, 1, 3, 11, 0, 2, 2, 1, 0, 15, 13, 2, 6, 15, 4, 8, 4, 12, 0, 2, 12, 1, 5, 6, 6, 12, 8, 0, 10, 5, 8, 15, 4, 10, 0, 4, 1, 4, 9, 1, 2, 0, 6, 8, 2, 1, 7, 5, 2, 1, 6, 6, 2, 1, 7, 6, 2, 1, 6, 6, 2, 1, 7, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1, 6, 6, 2, 1]Dapat kita lihat, dari generasi keystream hasil diatas, hasil dari Logistic Map menghasilkan deret yang benar-benar repetitif secara statis dan periodik.
Dari eksperimen tersebut, dapat kita catat nilai mana saja pada konstanta r yang menyebabkan keystream yang repetitif.
Daftar konstanta r yang berpotensi menghasilkan keystream statis adalah:
1.1 ~ 2.4
2.6 ~ 2.8
3.3Sedangkan, daftar konstanta r yang berpotensi menghasilkan keystream periodik adalah:
2.5
2.9
3.1
3.2
3.4
3.5Dari dua fenomena diatas, dapat disimpulkan bahwa ruang kunci dalam memilih konstanta r semakin terbatas untuk menghindari adanya repetisi keystream tersebut baik repetisi statis maupun periodik.
Sehingga konstanta r yang mungkin dipilih untuk menghindari repetisi adalah dengan memilih salah satu dari nilai berikut.
1.0~
3.0~
3.6~
3.7~
3.8~
3.9~Untuk nilai 0.9 kebawah diabaikan karena setelah beberapa proses generasi, nilainya akan cenderung menuju 0, sehingga tidak mampu membangkitkan keystream dengan ukuran besar.
Jadi, untuk mendapatkan keystream dinamis dari Logistic Map, pertama kita cek apakah terdapat repetisi pada pixel-pixel cipher image-nya (terutama pada koordinat bawah). Untuk repetisi statis, kita cukup melakukan brute-force 1 dari 16 kemungkinan nilai saja, sedangkan untuk repetisi periodik, kita cukup melakukan brute-force 2 sampai 4 dari 16 kemungkinan nilai.
Sedangkan jika tidak terdapat tanda adanya repetisi bit keystream, kita dapat melakukan brute-force untuk mencari nilai konstanta r dari kemungkinan daftar nilai yang tidak mengakibatkan repetisi tadi beserta nilai awal x0.
Proof of Concept
Implementasi lengkap dari skenario ini dapat dilihat di link ini
Conclusion
Dari kedua skenario implementasi diatas, dapat disimpulkan bahwa skema kriptosistem berbasis chaos ini benar-benar rentan terhadap Chosen-Plain image Attack (Known-Plain image Attack juga dapat dilakukan di beberapa kondisi).
Baik fungsi Arnold’s Cat Map, Logistic Map, maupun penggunaan enkripsi selektif yang digunakan terdapat celah keamanan yang dapat membuat attacker mendekripsi gambar apapun yang terenkripsi tanpa akses ke secret key yang digunakan. Sehingga pengembangan lebih lanjut perlu dilakukan untuk dapat menghasilkan algoritma yang lebih baik lagi, khususnya dalam segi keamanan.
References
- Munir, Rinaldi. (2012). ANALISIS KEAMANAN ALGORITMA ENKRIPSI CITRA DIGITAL MENGGUNAKAN KOMBINASI DUA CHAOS MAP DAN PENERAPAN TEKNIK SELEKTIF. JUTI: Jurnal Ilmiah Teknologi Informasi. 10. 89. 10.12962/j24068535.v10i2.a310.
- Boeing, G. (2016). Visual Analysis of Nonlinear Dynamical Systems: Chaos, Fractals, Self-Similarity and the Limits of Prediction. Systems, 4 (4), 37. doi:10.3390/systems4040037